Entre los números que presentan curiosidades matemáticas destaca el 142.857 (ciento cuarenta y dos mil ochocientos cincuenta y siete). Este número tiene la particularidad que al ser multiplicado por la secuencia de 2 a 6, el producto resultante corresponde exactamente a las mismas cifras del número original pero en otro orden. Por esta razón, este tipo de números se denominan cíclicos.
Secuencia inicial
Véase la secuencia (separador de miles retirado para mayor claridad):
- 142857 × 2 = 285714
- 142857 × 3 = 428571
- 142857 × 4 = 571428
- 142857 × 5 = 714285
- 142857 × 6 = 857142
Otras curiosidades
Al multiplicarlo por 7, la particularidad anterior no se cumple, pero también el resultado es curioso:
-
- 142857 × 7 = 999999
Al continuar multiplicando, la particularidad antes descrita permanece, pero un poco menos evidente:
-
- 142857 × 8 = 1142856
Obsérvese que la cifra 7 ha desaparecido, pero ha sido reemplazada por 1 y 6: 1+6=7
-
- 142857 × 9 = 1285713 (Ahora falta el 4, pero queda 1 y 3)
- 142857 × 10 = 1428570
- 142857 × 11 = 1571427 (Falta un 8, pero tenemos un 1 y 7 adicionales)
-
- Si se sigue con la secuencia de multiplicaciones será posible encontrar aún otras permutaciones y combinaciones de cifras que volverán a componer el número original: 142857.
Por ejemplo:
-
- 142857 × 2 × 3 × 4 × 5 × 6 = 102857040
Este número es la parte periódica de un número que es dividido entre 7 (y no da exacto)
-
- Sea cual sea el número, estos seis números se repetirán siempre en el mismo orden, pero empezando desde uno u otro.
Si elevamos los primeros 3 dígitos al cuadrado, y lo restamos del cuadrado de los últimos 3 dígitos, nos llevamos otra sorpresa:
-
- 1422 = 20164
- 8572 = 734449
- 734449 − 20164 = 714285
Si sumamos los primeros 3 dígitos y los últimos 3 dígitos, obtendremos otro resultado curioso:
-
- 142 + 857 = 999
Si sumamos los digitos de 2 en 2, obtendremos otro:
-
- 14 + 28 + 57 = 99

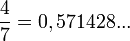
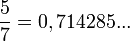
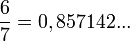



















1 comentarios:
ehhhh.que buen Número. no sabia de esto. muy bueno!
Publicar un comentario