Triángulo de T

Esto me lo enseñó Sandro (matemático autodidacta mendocino), me sirvió para rendir Algebra:

El Triángulo de Pascal (también conocido como triángulo de Tartaglia) es un triángulo formado por números enteros que es bien conocido por gran cantidad de gente al aparecer en los libros de texto desde secundaria en adelante. De todas formas vamos a ver cómo se construye:

Construcción del Triángulo de Pascal

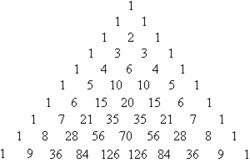
Colocamos un 1 en el vértice superior del triángulo. Despues, en la fila inferior, colocamos un 1 a la derecha y un 1 a la izquierda del 1 de arriba. En la inferior colocamos un 1 a cada extremo y entre los dos unos colocamos un 2 (1 + 1). En la inferior un 1 en cada extremo y en medio un 3 entre el 1 y el 2 (1 + 2) y otro 3 entre el 2 y el 1 (2 + 1). Y así sucesivamente: en los extremos un 1 a cada lado y en las posiciones intermedias colocamos la suma de los números de arriba. Queda una cosa así:

Su aplicación más importante es la siguiente: cada fila del triángulo representa los coeficientes de los monomios que aparecen en el desarrollo del binomio (a + b)ⁿ (tomando el 1 de arriba como la potencia n = 0), o lo que es lo mismo, los coeficientes que aparecen en el binomio de Newton coinciden con los elementos que aparecen en cada fila del triángulo de Pascal. Una propiedad realmente interesante. En la Wikipedia podéis ver más información.

Pero en el título del post aparece también la sucesión de Fibonacci. Este número y la sucesión de Fibonacci están íntimamente relacionados, ya que es el límite de la sucesión formada por los cocientes de cada elemento de la sucesión y el inmediatamente anterior.