Aunque existen numerosas expresiones que reciben el nombre de "conjetura de Ramanujan", existe una particularmente influyente sobre los trabajos sucesivos. Esta conjetura de Ramanujan es una aserción referente a las dimensiones de los coeficientes de la función Tau, una típica forma cúspide en la teoría de las formas modulares. Y ha sido finalmente demostrada posteriormente como consecuencia de la demostración de la conjetura de Weil mediante un complicado procedimiento.
Fórmulas
Entre muchas otras, Rāmānujan ha aportado la siguiente fórmula:
Se trata de una especie de obra de arte matemática donde se conecta una serie matemática infinita y una fracción continua para aportar así una relación entre dos célebres constantes de matemáticas.
Una segunda fórmula, demostrada en 1985 por Jonathan y Peter Borwein, es la que descubrió el en 1910 :
Es muy eficaz porque ella aporta 8 decimales a cada iteración.
Número de Rāmānujan
Se denomina número de Hardy-Ramanujan a todo entero natural que se puede expresar como la suma de dos cubos de dos maneras diferentes. Hardy comenta la siguiente anécdota :
- "No", me respondió, este es un número muy interesante; es el número más pequeño que podemos descomponer de dos maneras diferentes con suma de dos cubos.
G.H. Hardy
En efecto, 93 + 103 = 13 + 123 = 1729.
- Otros números que poseen esta propiedad habían sido descubiertos por el matemático francés Bernard Frénicle de Bessy (1602-1675) :
- 23 + 163 = 93 + 153 = 4104
- 103 + 273 = 193 + 243 = 20683
- 23 + 343 = 153 + 333 = 39312
- 93 + 343 = 163 + 333 = 40033
- El más pequeño de los números descomponibles de dos maneras diferentes en suma de dos potencias a la cuarta es 635 318 657, y ha sido Euler (1707-1763) quien le descubrió :
- 1584 + 594 = 1334 + 1344 = 635318657
Se denomina nésimo número Taxicab, denotado como Ta(n) o Taxicab(n), al más pequeño número que puede ser expresado como una suma de dos cubos positivos no nulos n de dos maneras distintas al orden de los operandos. Tal que, Ta(1) = 2 = 13 + 13, Ta(2) = 1729 y Ta(3) = 87539319. Variante del taxicab es el cabtaxi (un número cabtaxi es definido como el más pequeño número entero que se pueda escribir de n maneras diferentes (en el orden de los términos aproximados) como suma de dos cubos positivos, nulos o negativos).
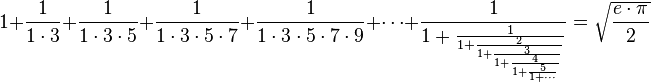
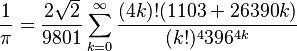



















0 comentarios:
Publicar un comentario